A 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊Check out this tutorial to learn about triangles!If you know the short leg length multiply by two for the hypotenuse length If you know the short leg then multiply by √3 for the long leg length If you know the long leg length divide by √3 for the short leg length The area of a triangle equals 1/2base * height
Right Triangles Gmat Free
Rules of 30 60 90 triangle
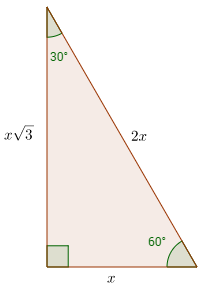
Rules of 30 60 90 triangle-30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 x Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63



How To Use The Special Right Triangle 45 45 90 Studypug
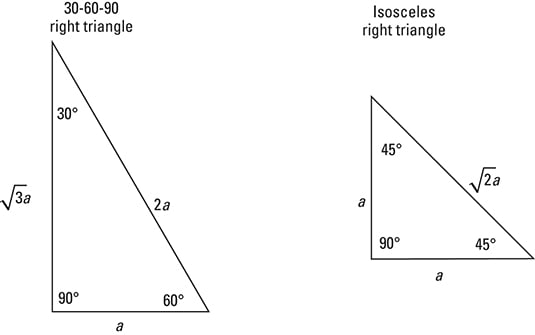
The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to useTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below Qualities of a Triangle A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a
Triangle30 60 90 This printable triangle has angles of 30, 60, and 90 degrees at its vertices Please make sure to print at 100% or actual size so the rulers will stay true to size Triangle Rules How do we know that the side lengths of the triangle are always in the ratio 1 3 –√ 2 ?Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles
A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleSpecial right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangleWhile we can use a geometric proof, it's probably more helpful to review triangle properties, since knowing these properties will help you with other geometry and trigonometry problems




30 60 90 Triangle Calculator Formula Rules



Trigonometry For Dummies Cheat Sheet Dummies
Rules for Special Right Triangles There are two special types of right triangles that we will be studying, the , and the 45 – 45 – 90 30 – 60 – 90 This type of triangle is also isosceles Rules for the Right Triangle If given one of the legs, multiply one leg by √2 to find the hypotenuseUsing what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected itemA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!



Special Right Triangles Ck 12 Foundation




The Complete Guide To The 30 60 90 Triangle
30 60 90 Right Triangle Calculator Short Side a Input one number of input area Long Side b Hypotenuse c Area Perimeter Input one number then click "calculate" button!Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI



45 45 90 And 30 60 90 Triangles Zona Land Education




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
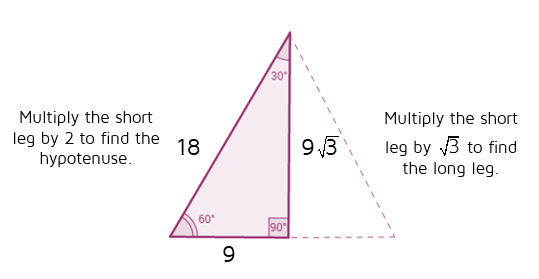
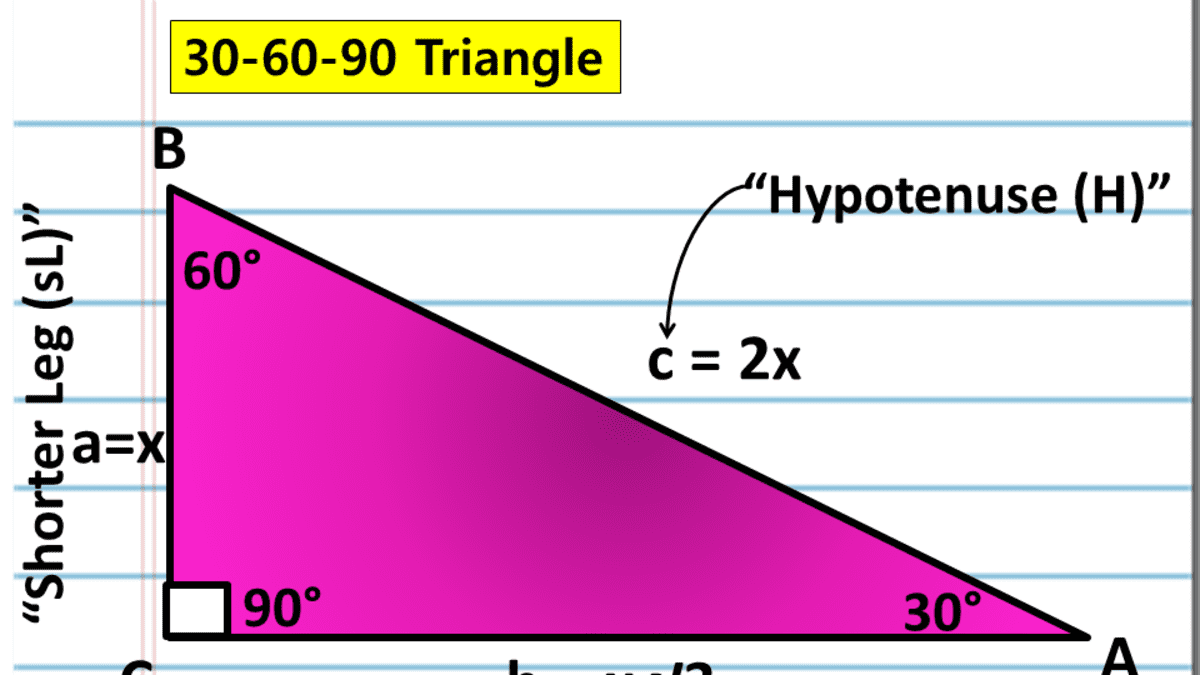
In any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, and you can find the length of the long leg by multiplying the short leg by the square root of 3A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andThe 45 45



30 60 90 Triangles P4 Kate S Math Lessons
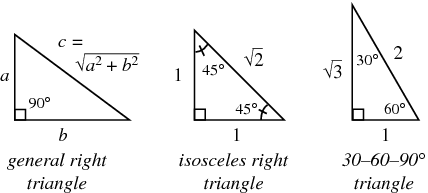



Right Triangle From Wolfram Mathworld
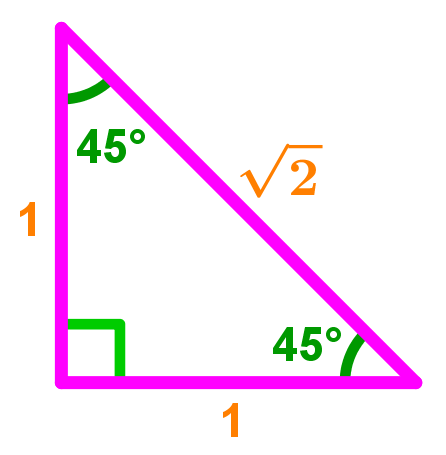
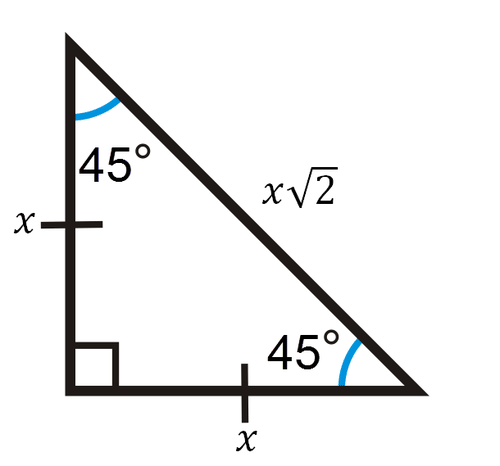
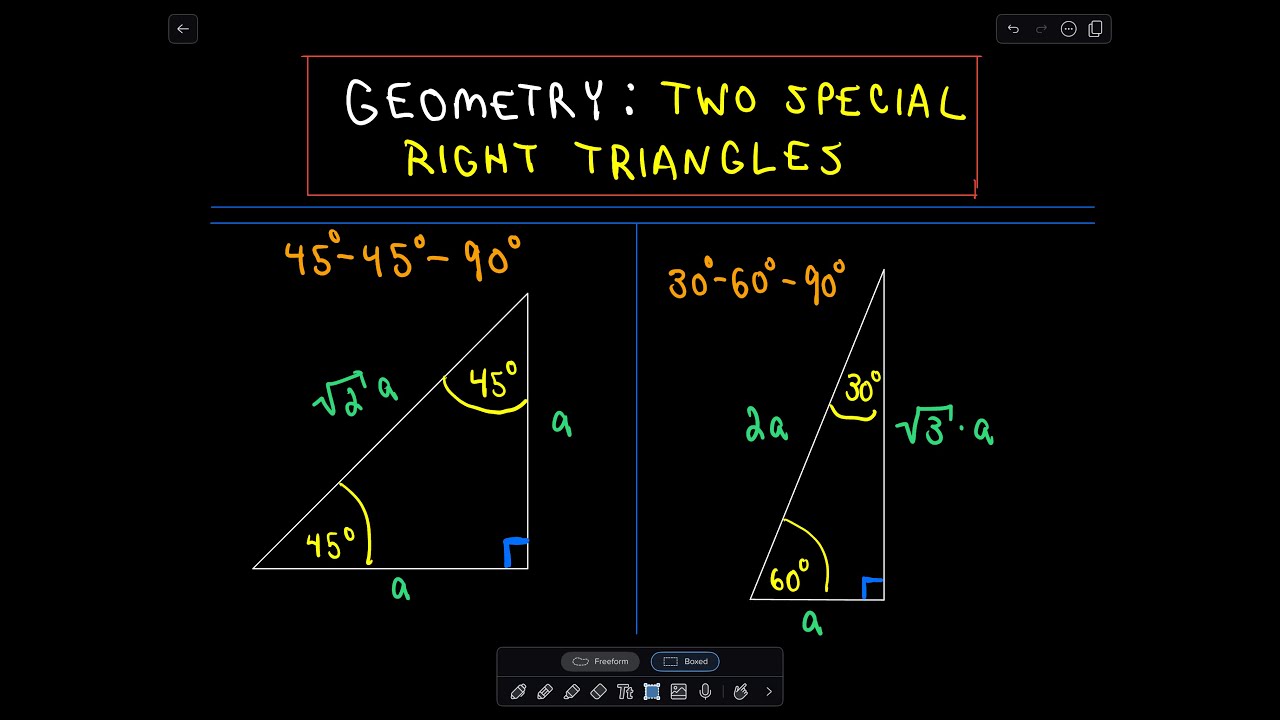
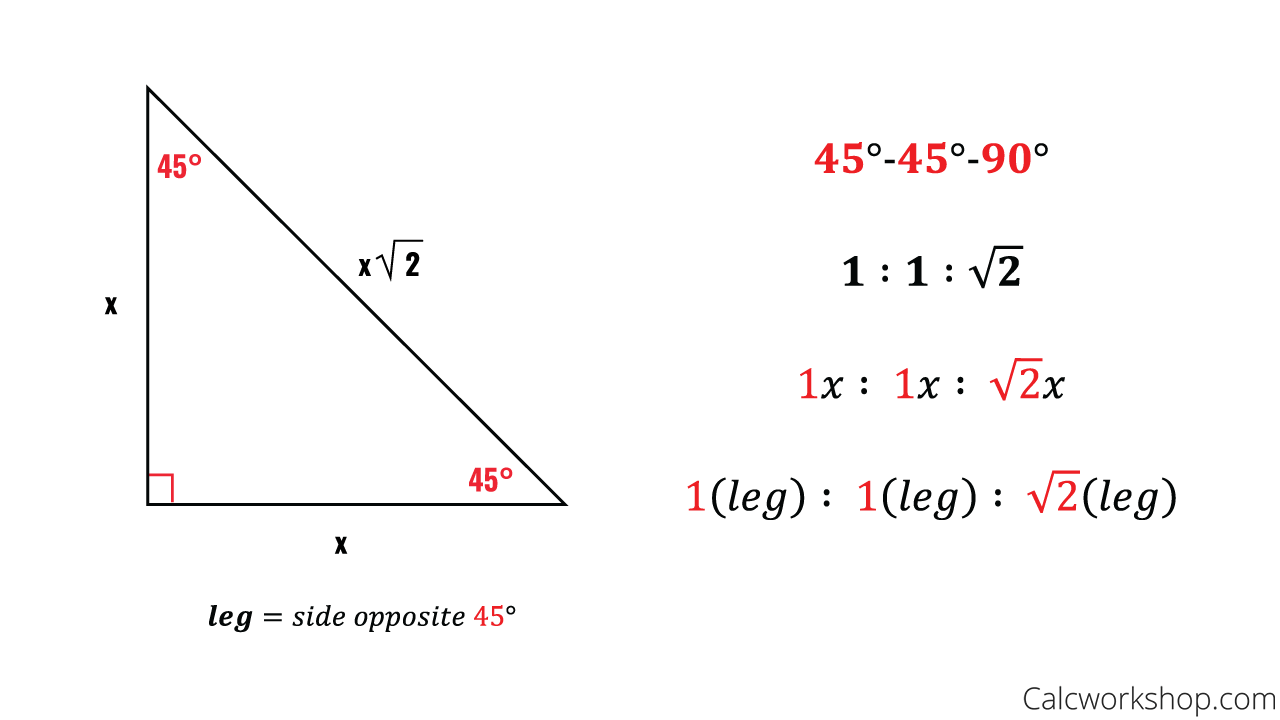
BronaGrand Triangle Ruler Square Set, 30/60 and 45/90 Degrees, Set of 2 44 out of 5 stars 79 $5 $5 Get it as soon as Wed, Mar 10 FREE Shipping onThis page shows to construct (draw) a 30 60 90 degree triangle with compass and straightedge or ruler We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angleBecause the interior angles of a triangle always add to 180 degrees, the third angle must45 45 90 Triangle Rules 1) The three internal angles are 45, 45, and 90 degrees 2) The legs are congruent 3) The hypotenuse length is √2 times the leg length 4) It can be created by cutting a square in half at the diagonal as shown below




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
The triangle ratios {eq}cos (30)=\frac {adjacent} {hypotenuse} {/eq} {eq}cos (30)=\frac {\sqrt {3}} {2} {/eq} {eq}sin (60)=\frac {opposite} {hypotenuse} {/eq} {eq}sin (60)=\frac {\sqrtPrintable stepbystep instructions for drawing a triangle with compass and straightedge or ruler Math Open Reference Home Contact About Subject Index Constructing a triangle This is the stepbystep, printable version If youDimensions of 30 60 90 triangle What is 30 60 90 triangle What are the formulas for a 30 60 90 triangle Hi Ron, it depends on which side is the base If the opposite side at the angle of 30 degrees in a triâgle has a length unit 1, the hypotenuse has the duration 2 units and the third side has length units



Fastest What Is The Rule For A 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
The reason these triangles are considered special is because of the ratios of their sides they are always the same!4 rows The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short sideThis is an isosceles right triangle The other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Common examples for the lengths of the sides are shown for each below The Triangle




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangle Definition Theorem Formula Examples
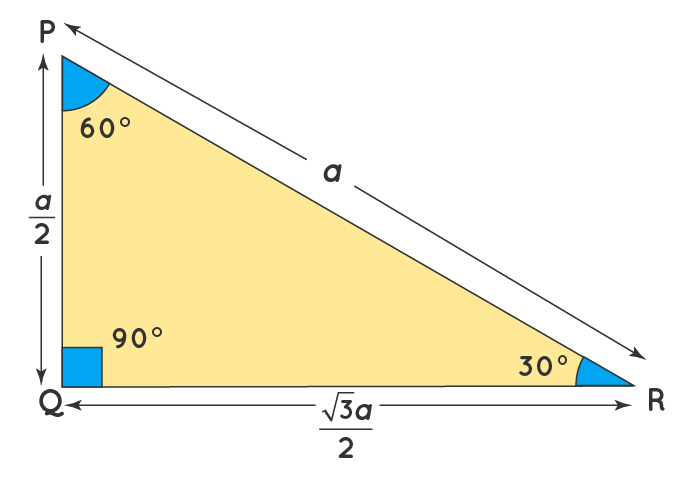
We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a 2 b 2 = c 2 1 2 ( 3) 2 = 1 3 = 4 = c 2 4 = 2 = c Using property 3, we know that all triangles are similar and their sides will be in the same ratio Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is3 rows As one angle is 90, so this triangle is always a right triangle As explained above that it is



Right Triangles Gmat Free




How To Use The Special Right Triangle 45 45 90 Studypug
The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?Area of a Triangle The formula to calculate the area of a triangle is = (1/2) × base × height In a rightangled triangle, the height is the perpendicular of the triangle Thus, the formula to calculate the area of a rightangle triangle is = (1/2) × base × perpendicular The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a Also, the unusual property of this 30 60 90 triangle is that it's the only right triangle with angles in an arithmetic progression



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
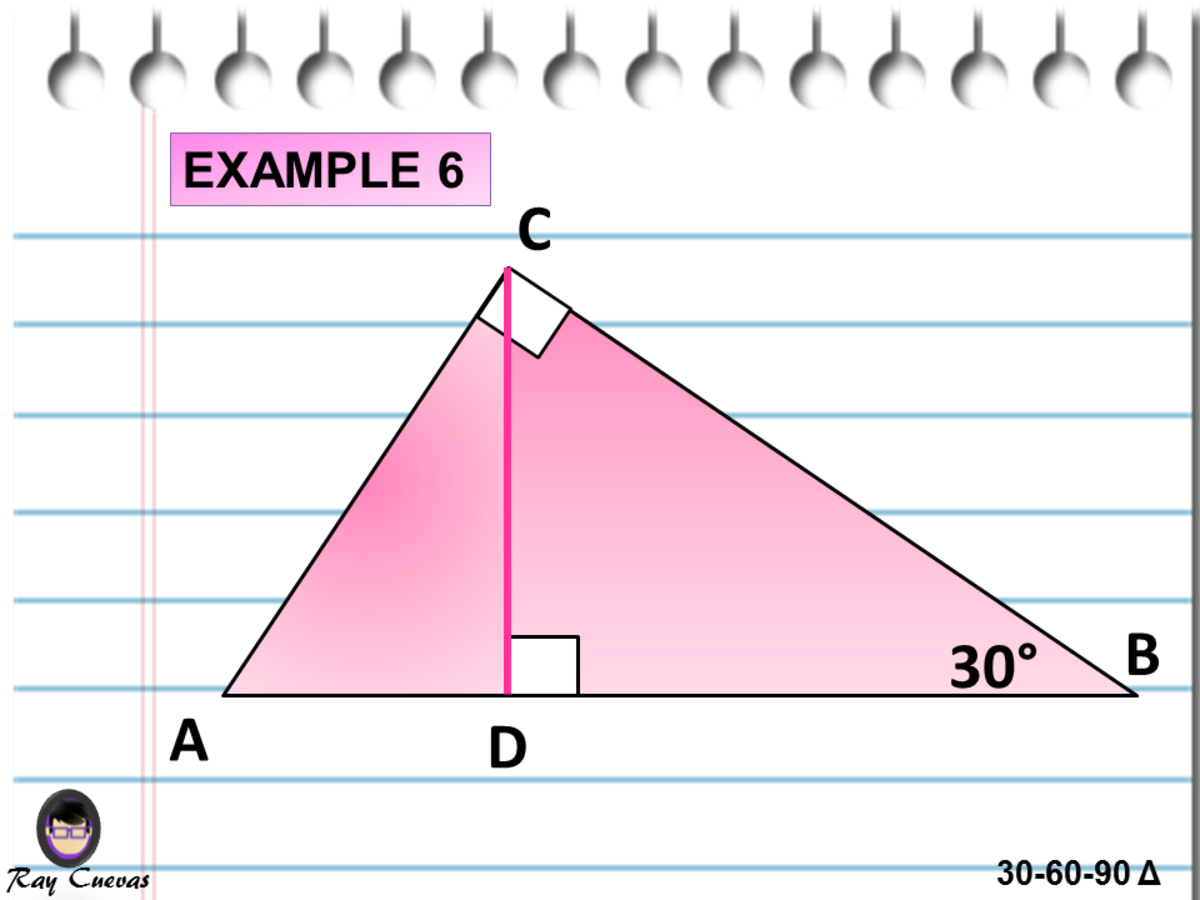
30 60 90 Triangle Formulas, Rules And Sides TL;DR Properties Of A Triangle A right triangle is a special right triangle in which one angle Right Triangles An Overview As stated previously, a right triangle is any triangle that has at least one right angle Right TrianglesGeometry Teachers Never Spend Time Trying to Find Materials for Your Lessons Again!Join Our Geometry Teacher Community Today!http//geometrycoachcom/GeometThe triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at
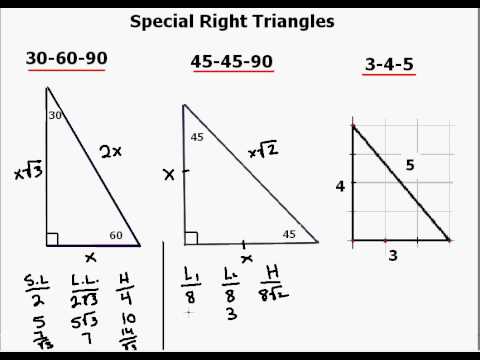



Special Right Triangle Explanation Youtube



1
30 60 90 Triangle Rules To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90 To solve for the side lengths, a minimum of 1 side length must already be known If we know that we are working with a right triangle, we know that one of the angles is 90 degreesThe 30 60 90 right triangle is a special case triangle with angles measuring 30 60 and 90 degrees 30 60 90 triangle in trigonometry And because this is a 30 60 90 triangle and we were told that the shortest side is 8 the hypotenuse must be 16 and the missing side must be 8 3 or 8 3 Transcript A few more triangle examples and an introduction to triangles Created by Sal Khan Special right triangles Special right triangles intro (part 1) Special right triangles intro (part 2) This is the currently selected item triangle example problem Practice Special right triangles




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




What Are The Angles Of This Triangle Mathematics Stack Exchange
Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for special right trianglesTriangle rules The main rule of triangles is that it has one right angle and while the other two angles each measure 45° 45 ° The lengths of the sides adjacent to the right triangle, the shorter sides have an equal length Another rule is that the two sides of the triangle or legs of the triangle that form the right angle We can see that this must be a triangle because we are told that this is a right triangle with one given measurement, 30° The unmarked angle must then be 60° Since 18 is the measure opposite the 60° angle, it must be equal to




Act Set 6 Special Right Triangle Rules Flashcards Quizlet




How To Find The Length Of The Hypotenuse Of A Right Triangle Pythagorean Theorem Sat Math




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




The 30 60 90 Triangle Topics In Trigonometry




How To Work With 30 60 90 Degree Triangles Education Is Around




Right Triangle Wikipedia
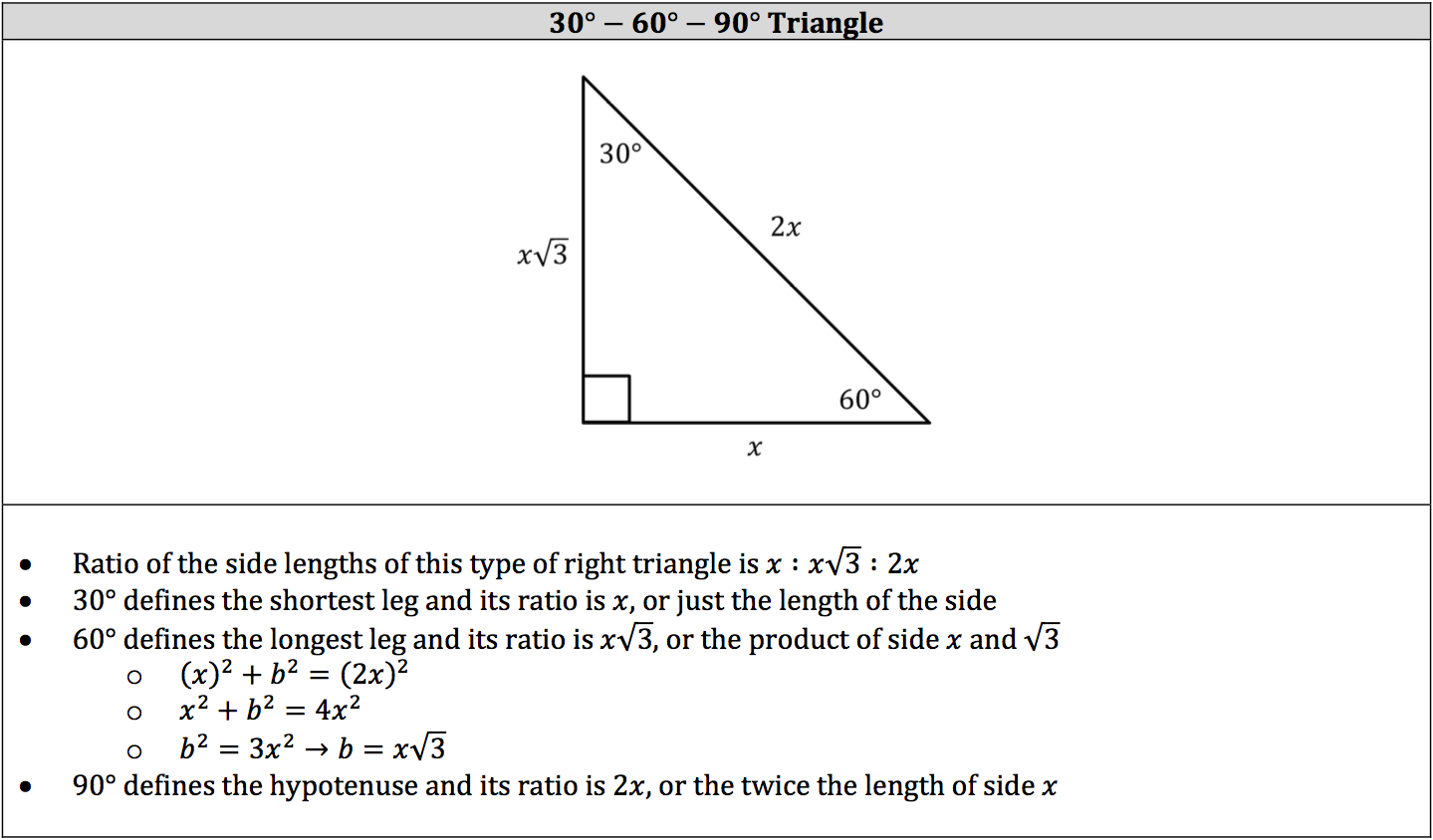



Isee Math Review Triangle Types And Rules Piqosity Adaptive Learning Student Management App
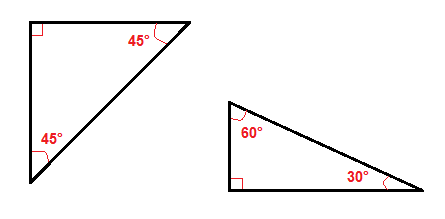



The Pythagorean Theorem Pre Algebra Right Triangles And Algebra Mathplanet




30 60 90 Triangles Spock S Guide To Math 4




30 60 90 Triangle Formulas Rules And Sides Science Trends
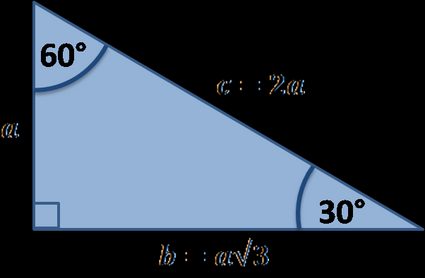



30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples
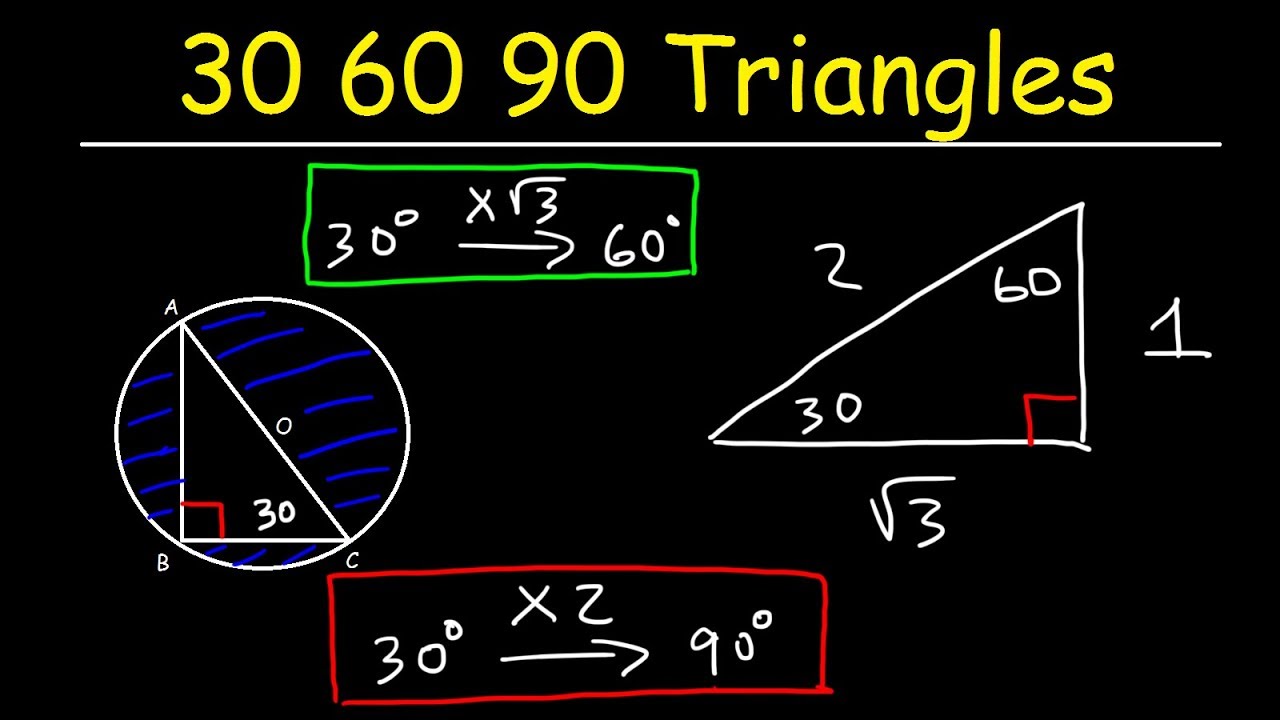



30 60 90 Triangles Special Right Triangle Trigonometry Youtube



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules



5 5 22 Special Right Triangles 30 60 90 Mosley Nc Math 2 Honors S2



1



Right Triangles Gmat Free



Right Triangles Gmat Free




Special Right Triangles Review Article Khan Academy




45 45 90 Triangle Calculator Formula Rules




30 60 90 Triangle Explanation Examples




The Unit Circle Ck 12 Foundation
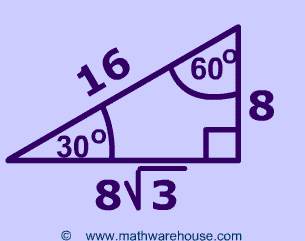



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




Obj To Calculate The Lengths Of Missing Sides By Using Templates Provided Illustrating The And The Right Triangles Ppt Download




The 30 60 90 Triangle Topics In Trigonometry




Act Set 6 Special Right Triangle Rules Flashcards Quizlet
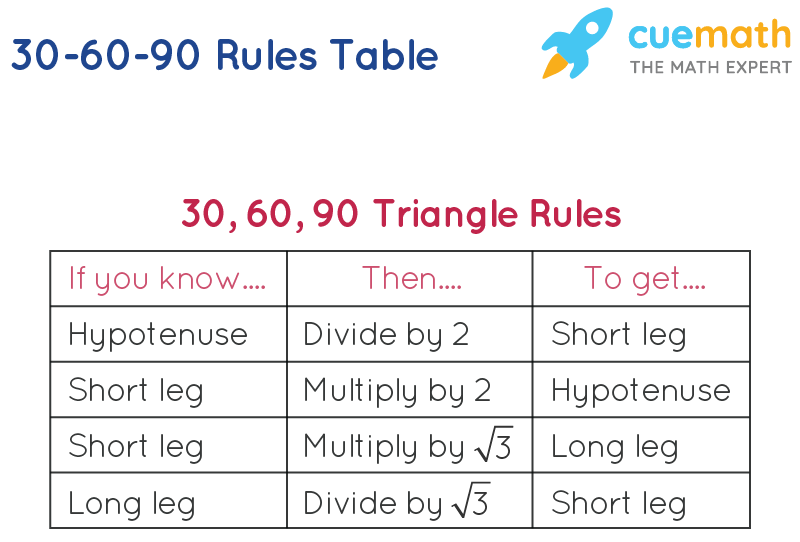



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




A Quick Guide To The 30 60 90 Degree Triangle Dummies
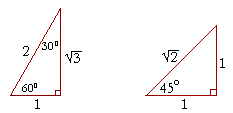



The 30 60 90 Triangle Topics In Trigonometry




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Right Triangles Free Math Help



45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangles Video Lessons Examples And Solutions



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube



1




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangles Fully Explained W 19 Examples



Non Right Triangle Trig




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
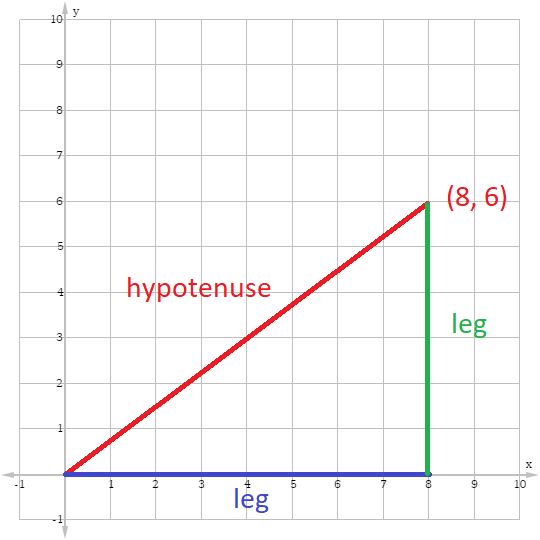



Fastest 30 60 90 Right Triangle Rules




3 4 5 Triangle Definition Math Open Reference




Triangles In Applied Problems Ck 12 Foundation



1
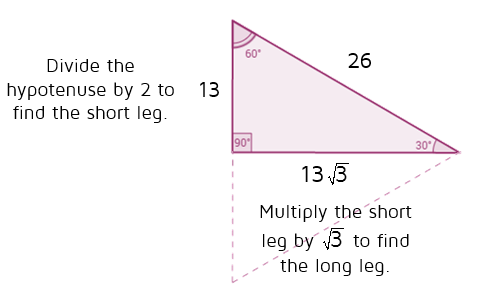



30 60 90 Triangles P4 Kate S Math Lessons




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules
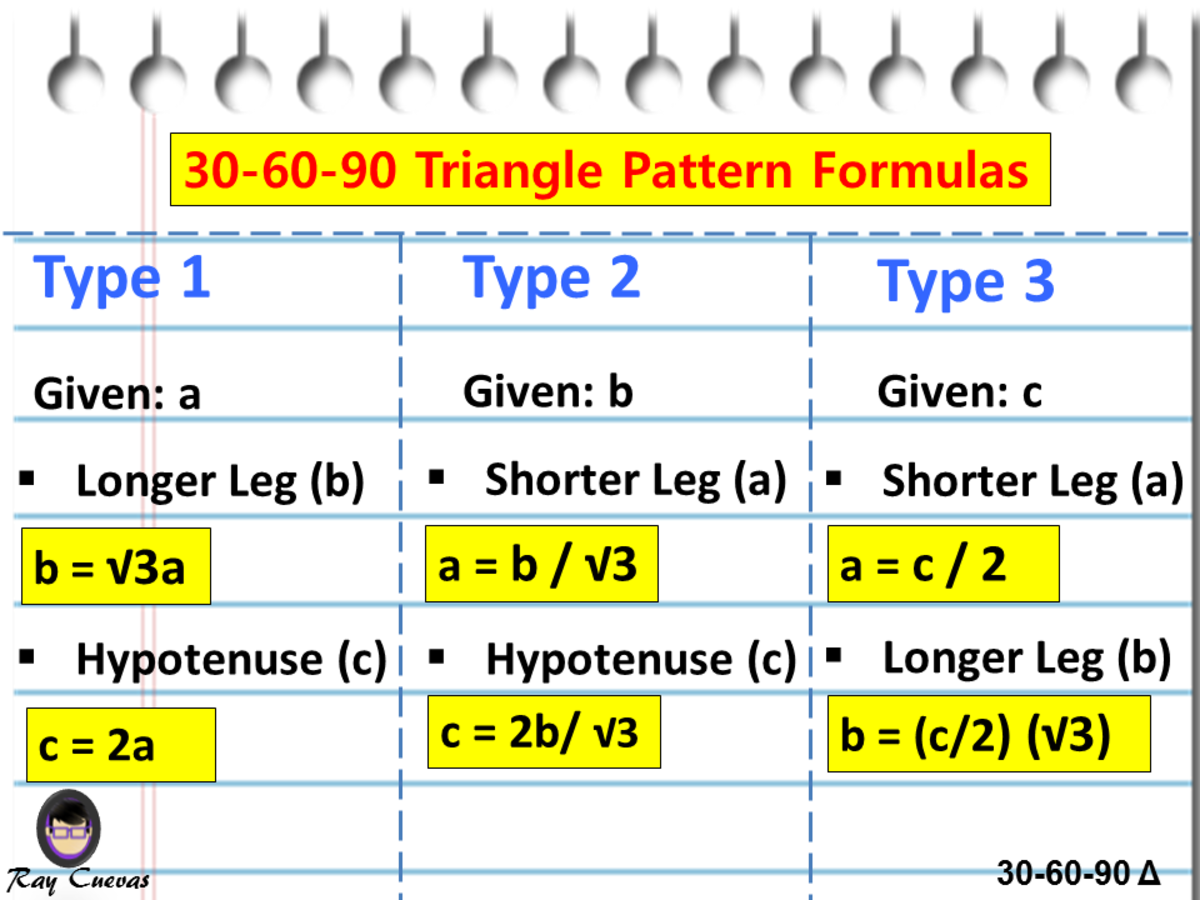



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles




Special Right Triangles Review Article Khan Academy
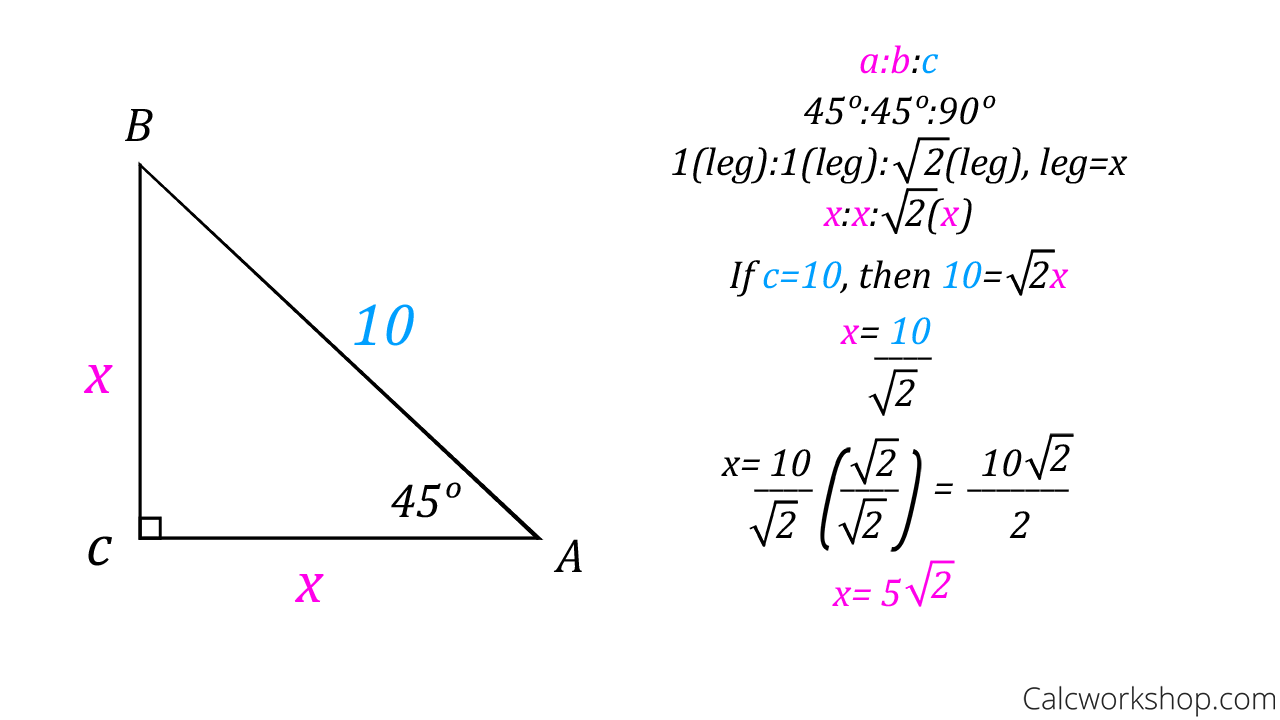



Special Right Triangles Fully Explained W 19 Examples




Right Triangle Wikipedia




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Sides Examples Angles Full Lesson




5 30 60 90 Triangles Geometry15a




Special Right Triangles Fully Explained W 19 Examples



Special Right Triangle 30 60 45 45 37 53 Elearning



How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Theorem Ratio Formula Video




The Complete Guide To The 30 60 90 Triangle




The Complete Guide To The 30 60 90 Triangle




Special Right Triangles Video Lessons Examples And Solutions
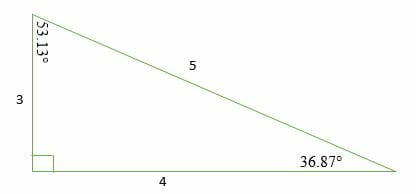



3 4 5 Right Triangles Explanation Examples
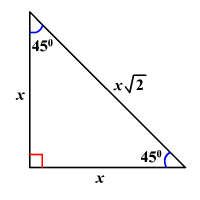



45 45 90 Triangles




30 60 90 Triangle Calculator Formula Rules




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
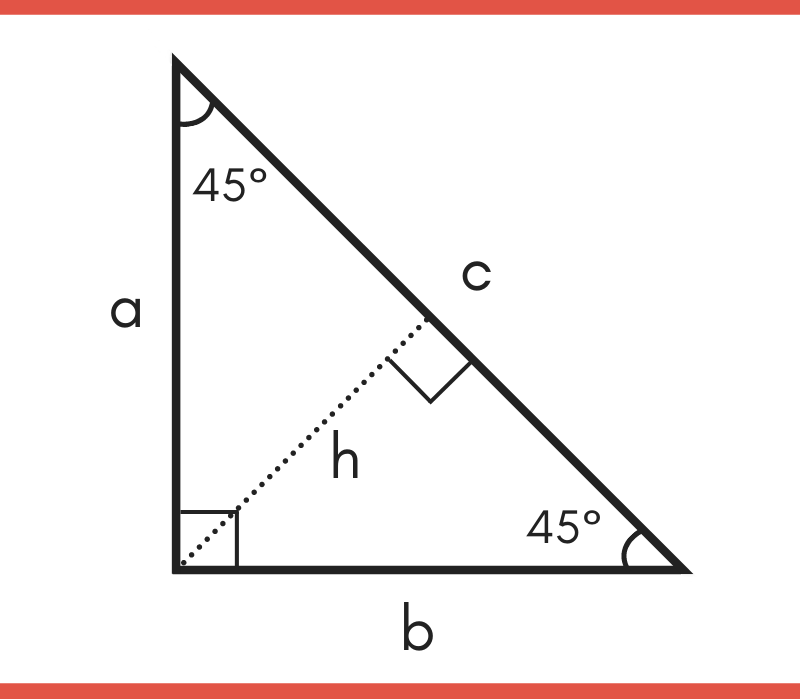



45 45 90 Special Right Triangle Calculator Inch Calculator




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
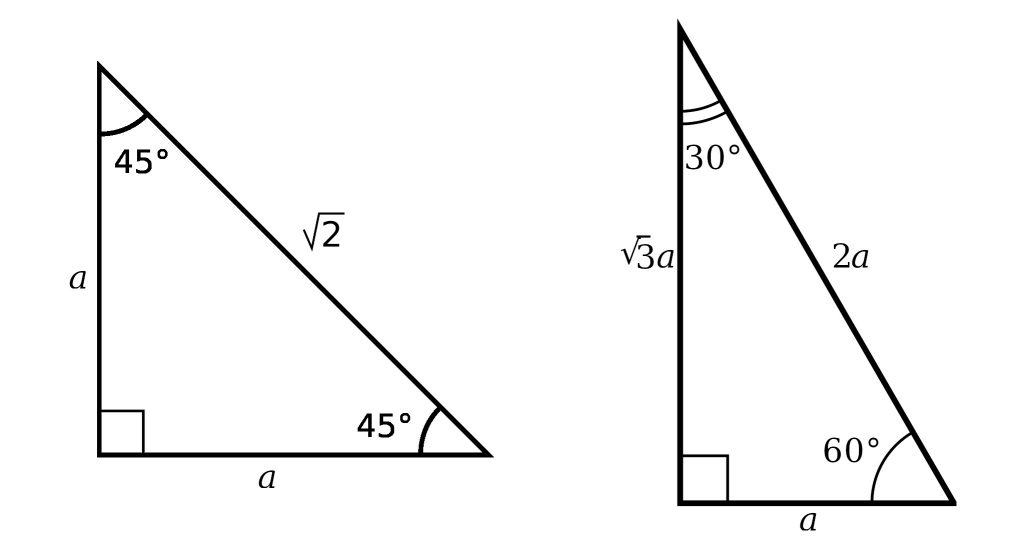



Special Right Triangles Sss a Examples Included



0 件のコメント:
コメントを投稿